

Ортогональный дизайн плотно укоренился во многих сферах человеческой жизни. Я думаю, не будет преувеличением сказать, что большинство людей, размышляя о доме своей мечты представляют его как совокупность ортогональных элементов. Такой выбор обусловлен отнюдь не эстетическими качествами прямоугольников и кубов. Заточенность производства конструктивных элементов на однообразные повторяющиеся операции, делает невозможным осуществление криволинейных архитектурных форм, по крайней мере в области типового строительства. Сложность инженерных расчетов и последующего контроля строительства оболочек двойной кривизны, также сильно ограничивают область применения данного типа конструкций. На фотографии ниже изображена инфраструктура федеральной разведывательной службы Германии.

Но было время, когда молодые люди, получившие образование в престижных учебных заведениях, устремились навстречу любви и гармонии в домах сферической формы. Главными распространителями идеи жизни в геодезических куполах считаются студенты Black Mountain College, где кстати, преподавал Бакминстер Фуллер - не первооткрыватель, но очень важный человек в истории легковесных сферических конструкций. Именно он долгое время обладал монополией на строительство геодезических куполов. Хотя на частное строительство патентные ограничения не распространялись.

Подготавливая материал для данной статьи, я наткнулся на информационный буклет в котором семейные пары и одинокие энтузиасты красочно рассказывают, как им хорошо живётся в таких домах. Что самое интересное, подборка материалов по геодезическим куполам также включала мнение некоторых из них после тридцати лет проживания под куполом. Все они описывают тот период, как самый худший в их жизни, в основном это связано с постоянными протечками купола и невозможностью применения адекватных утепляющих материалов. Ещё очень часто возникали проблемы с жилищными инспекциями. Тем не менее геодезические купола и сегодня используются для решения некоторых задач. Благодаря повышенной устойчивости к ветровым нагрузкам они прекрасно подходят в качестве укрывной конструкции, чему свидетельствует многолетнее противостояние Новороссийской РЛС на горе Колдун экстремальным погодным условиям в зимний период. Ещё одной отличительной особенностью куполов является тороидальное закручивание конвекционных потоков, что создаёт дополнительную теплоизоляцию. В связи с чем они всё чаще применяются для укрытия домов в полярных условиях. Ну и конечно, классическое применение геодезических куполов это садово-парковая архитектура. На фотографии ниже изображена РЛС на горе Колдун.

Геометрия геодезического купола строится на основе регулярного многогранника, выбор которого зависит от многих параметров. Наиболее популярным решением является икосаэдр, среди всех многогранников он даёт наиболее регулярное распределение точек на сферической поверхности. Хотя есть ситуации, когда регулярность является негативным фактором, например в укрывных конструкциях РЛС периодическая сетка купола может вносить искажения в получаемый сигнал. Построения регулярных геодезических сеток достаточно подробно описаны во многих открытых источниках, в данной статье мы рассмотрим пример построения псевдо-регулярной сетки, возможной к применению в небольших РЛС. Расчёты мы будем выполнять в среде Grasshopper с использованием компонента Python.
Как я уже говорил, в качестве основания сферического многогранника мы возьмем икосаэдр. Все построения можно выполнить вручную непосредственно в Rhinoceros. Я не рекомендую использовать готовые решения, просто потому, что построение регулярных многогранников - довольно интересная и в то же время простая тема. Следует уточнить, что центр многогранника находится в нулевой точке.
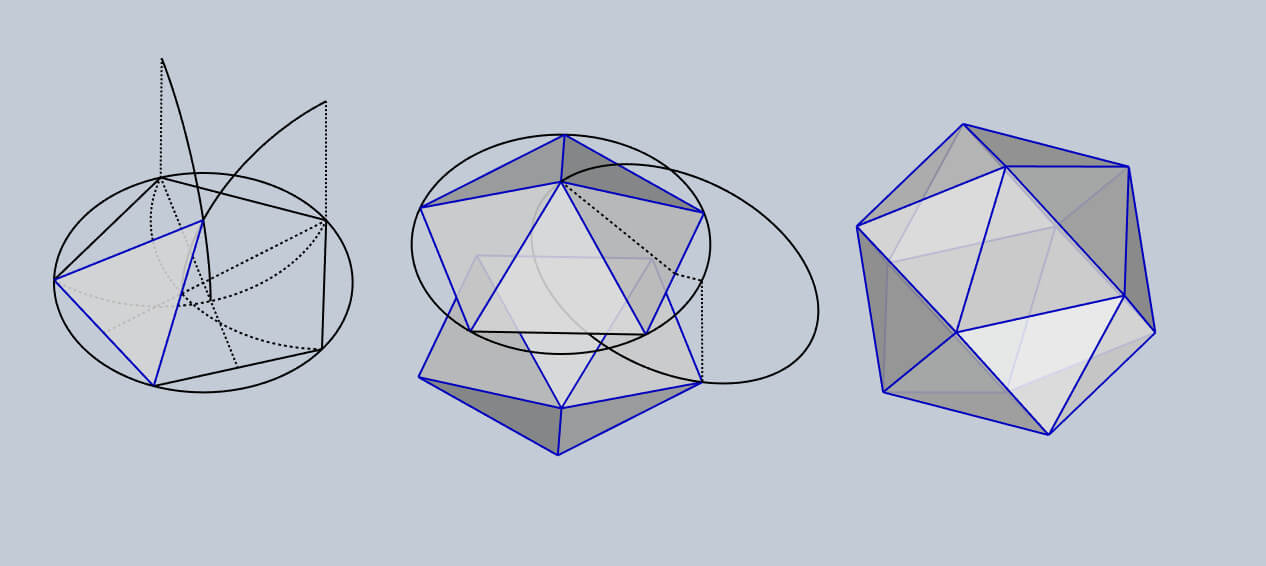

Теперь нужно выделить некоторую грань, её вершины лучше представлять как базовые векторы, интерполируя которые мы получаем начальное равномерное распределение точек. Вершины многогранника лежат на сфере некоторого радиуса, новые точки, также должны лежать на поверхности сферы. Для этого можно воспользоваться сферическими барицентрами, но так как в нашем случае количество вершин грани ограничено тремя, то можно воспользоваться попарной сферической интерполяцией. Если вам понадобится сферическая интерполяция грани с большим количеством вершин, знайте, такие методы существуют. Ссылку на их описание я приведу в конце статьи. На изображении ниже показана попарная сферическая интерполяция.
Создадим компонент Python, принимающий на вход x, y, z - базовые векторы (вершины грани), n - количество делений. В редакторе компонента нужно ввести следующее.
# секция импорта
import math
import functools as ft
import random as rnd
import ghpythonlib.components as ghДальше нам понадобится несколько векторных операций.
def vec_op(v1, v2, f): # общий бинарный оператор
if type(v2) == float:
return [f(a, v2) for a in v1]
else:
return [f(a, b) for a, b in zip(v1, v2)]
def vec_add(v1, v2): # сложение
return vec_op(v1, v2, lambda a, b: a + b)
def vec_mul(v1, v2): # умножение
return vec_op(v1, v2, lambda a, b: a * b)
def vec_div(v1, v2): # деление
return vec_op(v1, v2, lambda a, b: a / b)
def vec_len(v): # длина вектора
return math.sqrt(sum([x**2 for x in v]))
def vec_dot(v1, v2): # скалярное произведение
return sum([a*b for a, b in zip(v1, v2)])
def vec_angle(v1, v2): # угол между двумя векторами
return math.acos(vec_dot(v1, v2) / (vec_len(v1) * vec_len(v2)))Можно было воспользоваться решениями rhinoscript, но мне нужен угол в радианах. Далее идёт определение сферической интерполяции.
\[slerp(v_{1},v_{2}; p) = \frac{sin((1-p)a)}{sin(a)}v_{1}+\frac{sin(pa)}{sin(a)}v_{2}\]
def slerp(v1, v2, p):
if v1 == v2:
return v1
else:
a = vec_angle(v1, v2)
m1 = math.sin((1-p) * a) / math.sin(a)
m2 = math.sin(p * a) / math.sin(a)
return vec_add(vec_mul(v1, m1), vec_mul(v2, m2))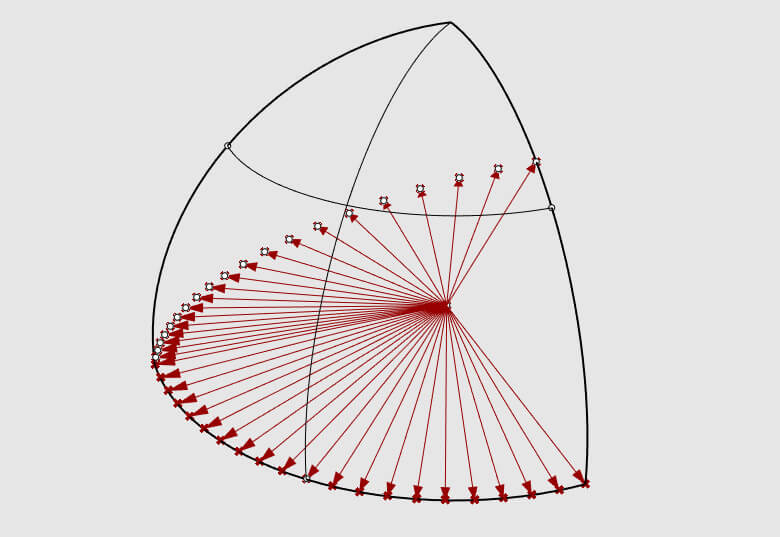
Алгоритм построения сетки разбит на две фазы. Сначала мы строим треугольник из точек.
# в результате функция выдаёт что-то типа
# [p8, p9]
# [p5, p6, p7]
# [p1, p2, p3, p4]
def tri_points(v1, v2, v3, n):
# n - количество делений
points = []
dx = 1 / (n-1)
# первое изопараметрическое направление
for k in range(n-1):
points.append([])
# второе изопараметрическое направление
# каждый раз количество требуемых точек уменьшается на одну
for j in range(n - k):
dj = 1 / (n-k-1)
# первая пара векторов
s1 = slerp(v1, v3, dx * k)
s2 = slerp(v2, v3, dx * k)
# искомая точка
sx = slerp(s1, s2, dj * j)
points[-1].append(sx)
# последняя сингулярная точка как частный случай
points.append([v3])
return pointsЗатем объединяем ряды точек в треугольники. Если вы когда нибудь программировали OpenGL, то у вас не должно возникнуть вопросов.
# функция смешивания треугольных рядов
# tri_comb([1, 1, 1], [2, 2, 2, 2]) = [2, 1, 2, 1, 2, 1, 2]
def tri_comb(a, b):
c = [a, b]
for n in range(len(a) + len(b)):
yield c[n % 2][int((n)/2)]
def tri_grid(pts):
tris = []
# проход по рядам точек
for k in range(len(pts) - 1):
# комбинируем два смежных ряда
c = list(tri_comb(pts[k], pts[k+1]))
# просто представляем точку как кортеж
gpts = [tuple(pt) for pt in c]
for j in range(len(c) - 2):
# формируем треугольники простым сдвигом
tris.append(gpts[j:j+3])
return tris
Теперь нам нужно модифицировать tri_grid так, чтобы она параллельно формировала шестиугольники. Сделаем мы это на основе двухмерной индексации и волшебства модульной арифметики. Если вы не знакомы с модульной арифметикой я рекомендую начать с замечательных книг Годфри Харди.
def tri_grid(pts):
hexa = []
free = []
idy = 0
for k in range(len(pts) - 1):
c = list(tri_comb(pts[k], pts[k+1]))
gpts = [tuple(pt) for pt in c]
idx = 0
for j in range(len(c) - 2):
tri = gpts[j:j+3]
hp = (j + (k % 2)) % 4
if hp != 0:
hexa.append((tri, (idx, idy)))
else:
free.append(tri)
if hp == 3:
idx = idx + 1
idy = idy + (k % 2)
return free, merge_hexagons(hexa)
Для рандомизации шестиугольника нужно сдвинуть его центр к случайной точке выбранной на периферии. Выполнить это немного сложнее чем представить.
# так как наши шестиугольники это всего лишь индексы,
# то нам необходимо преобразовать их в реальные группы треугольников
def merge_hexagons(hex):
hex.sort(key=lambda x: x[1])
ret = []
ph = None
for h in hex:
if h[1] == ph:
ret[-1].append(h[0])
else:
ret.append([])
ret[-1].append(h[0])
ph = h[1]
return ret
# декомпозиция точек на периферию и центр
def decompose(h):
cen = list(ft.reduce(lambda x, y: x.intersection(y), [set(t) for t in h]))[0]
per = list(set([pt for tri in h for pt in tri if pt != cen]))
return cen, per
# функция замещающая вершину шестиугольника
def replace_center(hex, old, new):
new_hex = hex
for n in range(len(hex)):
hex[n] = [new if pt == old else pt for pt in hex[n]]
# рандомизация шестиугольников
def randomize_hexagons(hex):
for h in hex:
cen, per = decompose(h)
vec = rnd.choice(per)
npt = slerp(cen, vec, 0.5)
v.append(gh.ConstructPoint(*npt))
replace_center(h, cen, npt)Теперь собираем всё вместе.
# треугольник из точек
points = tri_points(list(x), list(y), list(z), 10)
# шестиугольники и остаточные треугольники
free, hexagons = tri_grid(points)
# вносим случайные изменения
randomize_hexagons(hexagons)
# Строим полигоны
for hex in hexagons:
a.extend([gh.PolyLine([gh.ConstructPoint(*pt) for pt in pts], True) for pts in hex])
Если мы имеем дело с плотными сетками, то данную процедуру можно запустить рекурсивно на нескольких уровнях деления. В результате чего мы получим более хаотичную структуру. Функцию рандомизации я зафиксировал на конкретном параметре. Таким образом каждый шестиугольник является повернутой копией другого. Это необходимо для минимизации затрат связанных с производством большого числа разнообразных элементов. Хотя в действительности всё зависит от инструментальных требований конкретного технологического процесса. Например, раскрой материала выполняемый с помощью ЧПУ не требует сопроводительных инструментов, поэтому типизация элементов для данного процесса не является существенной. В то время как формовочные процессы сильно зависят от затрат связанных с изготовлением пресс-форм, которые можно минимизировать посредством повторного использования. Геодезические купола формируются посредством раскроя. Исключением являются узловые элементы, но они, как правило, допускают большое число конфигураций. Так что, в современных условиях в проведении процедуры обширной оптимизации нет смысла. Ярким примером успешной работы с множеством разнотипных элементов является небоскрёб Aldar (фото внизу), при строительстве которого была применена технология QR-маркировки.

В следующих статьях я расскажу о методах BIM детализации полученной геометрии.
Spherical Barycentric Coordinates / Eurographics Symposium on Geometry Processing (2006)